I started attending a few Massive Open Online Course (MOOC) by edX in the last few months. In the last 4 months, I have completed 4 courses by edX. I would like to share my experience during attending this courses. I am really happy that I took my time to attend this courses. Two of the course were related to programming, "Introduction to Computer Science and Programming Using Python" and "Introduction to Computational Thinking and Data Science". These courses were provided by MITx. It was really a great experience to learn from professors of such an excellent institution.
In the first course, we are basically learning python we could say. Yet the ideas we learn from the course doesn't just bind to that particular language. So the course is more like an introduction to Computer Science using python as a tool. I was really able to gather a lot of new information regarding Computer Science and python programming from this course. But I don't like to share those stuff right in this post.
It was the second course which was a continuation of the first course attracted me more. Introduction to Computational Thinking and Data Science. What I felt is that after going through this course your programming skill set and method of tackling a problem improves greatly. Like the name suggest you would start tackling a problem in front of you more computationally. You also learn how to analyse available data and arrive at conclusions from that data.
I will split this into a few posts. So in this post, I would like to share one example in the course which attracted me more. A few things taught in this course is about using plotting tools for a nice and neat representation of data, creating simulations to solve problems, stochastic programming etc. In the process of learning, we deal with a lot of interesting problems like finding probabilities of coin tossing, dice rolling etc, solving the Monte Carlo problem etc. And then there was a simple nice example showing how to use the randomness to solve non-random problems.
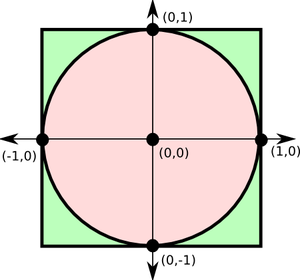To find a value of pi, there is a beautiful method described in this course. Consider a unit circle fit into a square of side 2. If you can't still imagine it take a look at the image.
Now imagine you are throwing a number of nails into this picture(Nails sand or whatever works for you). A number of nails will fall right into the circle(The pink area) and another number of nails will fall in outside circle.
The ratio between the number of nails inside the circle to the total number of nails thrown will be equal to the ratio between the area of circle and area of the square. That means
So if we can find the number of nails inside a circle we can use it to calculate the value of pi. To do this, we create a simulation. In the course, they used a class to define this setup. Anyway, I have used functions to do this simulation rather than class( I find it easier to work with functions).
First I created a function throw_nail(). It will generate two random numbers x and y using the random() function in the random module of python. These points represent x and y coordinate of the point where the nail has fallen. Now using the equation of a unit circle we can determine whether the point is inside the circle or outside the circle. We have
X2 + Y2 = 1
for a unit circle. Now substituting values of x and y, we can determine whether the nail is inside or outside the circle. Please not that random() generates a value between 0 and 1 with equal probability. This function is added below.
def throw_nail():
x = random()
y = random()
if (x**2 + y**2) < 1:
return 1
else:
return 0
1 indicates nail is inside the circle 0 indicates nail is outside circle(I should have used True and False to return, but I am used with programming in c and some habits won't change I think). Now this represents a single nail. Repeat this process for multiple nails. For this, I created a function simulate() which has one argument, an integer which represents the number of nails to be thrown. Inside this simulate() function, throw_nail() will be called n times(n the argument of simulate). And according to the returned value, a variable tracking the number of nails fallen inside the circle will be updated. After this ratio between the number of nails inside the circle and the total number of nails(n) multiplied by 4 will be returned. It is supposed to be the value of pi according to our assumption. I will add the simulate function and the output when 10000 nails are thrown.
def simulate(n):
inside = 0.0
total = 0.0
for i in xrange(n):
if throw_nail() == 1:
inside += 1
return 4*inside/(n)
Output when "print simulate(10000)" was
3.1244
It's close enough to value of pi. But is it good enough? Let's run this simulation once again and see the output.
3.148
It's better. But now the value is changed from the previous. And we will probably get different answers each time we run this function. But we can say it got a one decimal place precision. Because the part 3.1 doesn't change. Now if we increase the number of nails we will get a better answer. To show this, I made a program to simulate throwing a different number of nails(100,1000,10000,10000) and simulated each case for 1000 times. The output of each case are stored and a histogram was made. Refer the image below
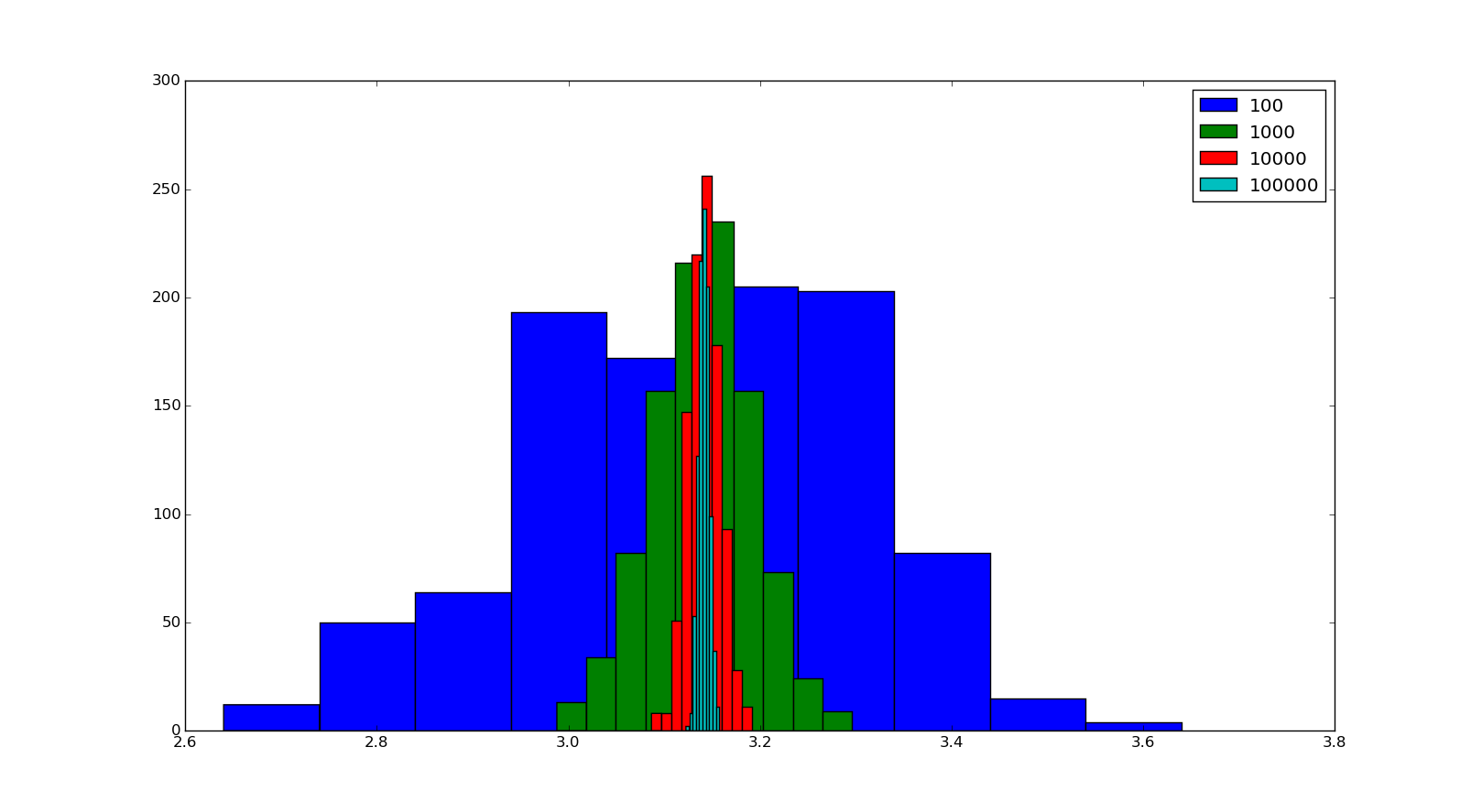
As you can see in the image, when the number of nails increases the range of value of pi becomes more precise. When a 100 nails simulation was done the range of values is from 2.6 to 3.6. But when a 100000 nails simulation is done values is in the range 3.12 to 3.16. Also, more values are in the range 3.14 to 3.145. If we increase the number of nails furthermore we will get a more precise value of pi. The only problem is it will take more time. To get a precision of four decimal places, it will take around 1 hour for the simulation. Maybe if you use c for coding you could increase simulation time considerably.
This method is actually called Monte Carlo simulation to calculate the value of pi. Simply search that in google or YouTube and you can learn more on this topic.